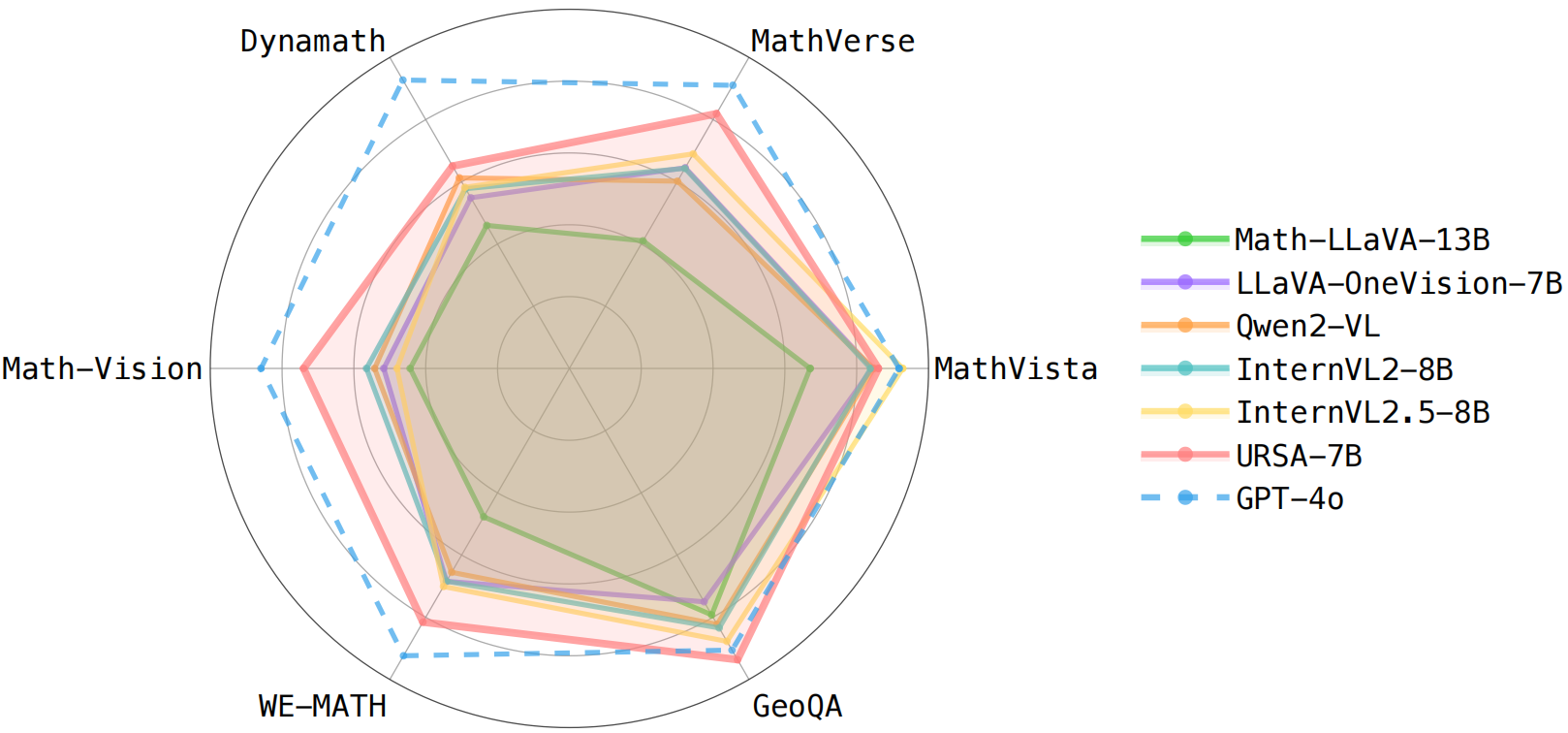
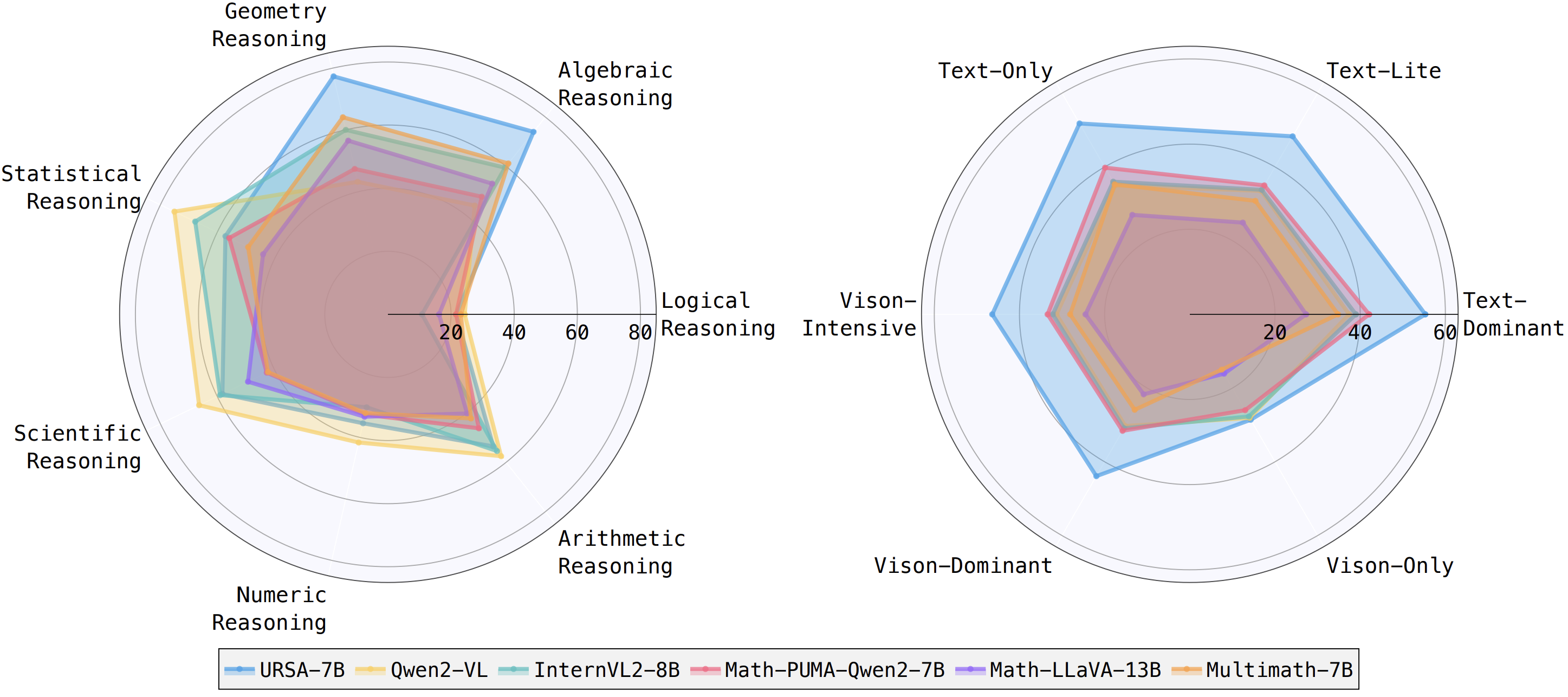
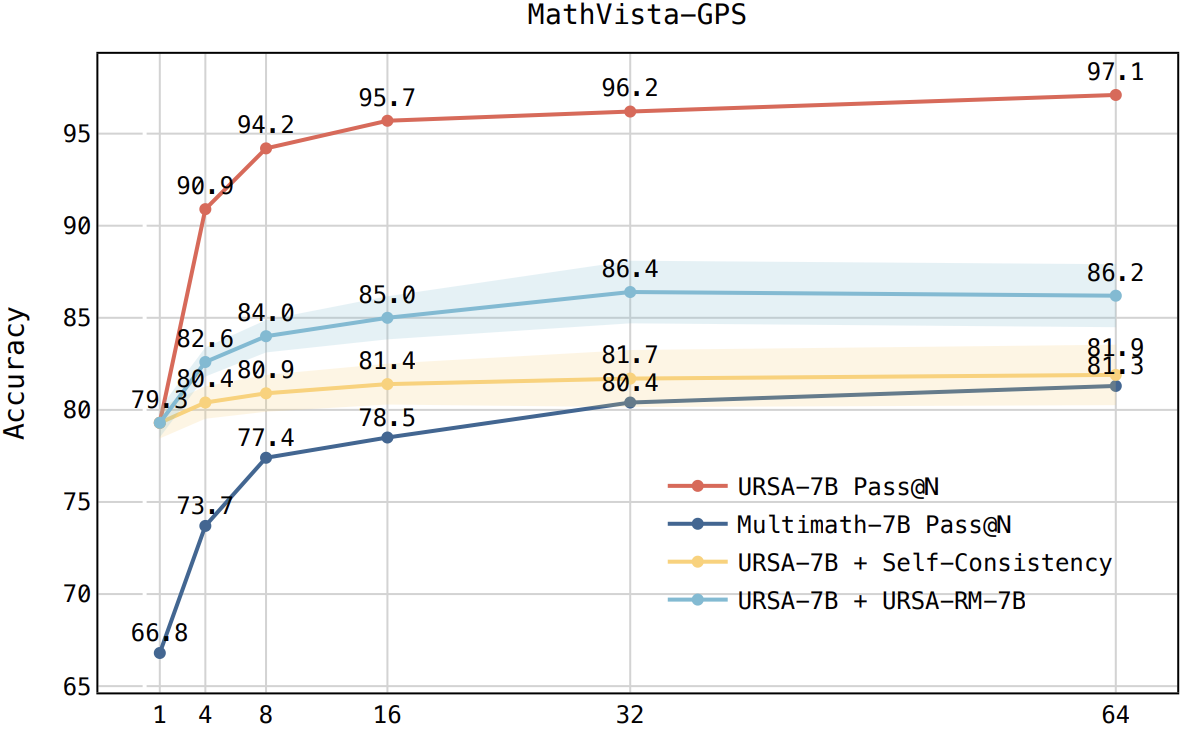
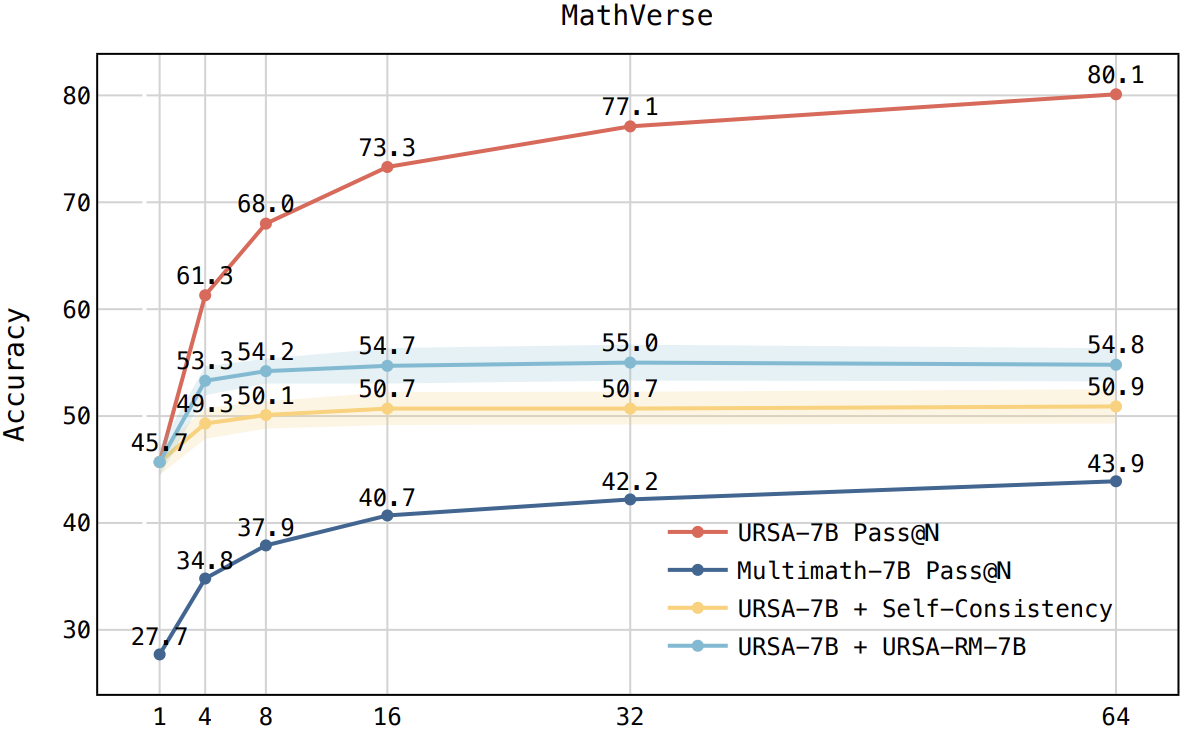
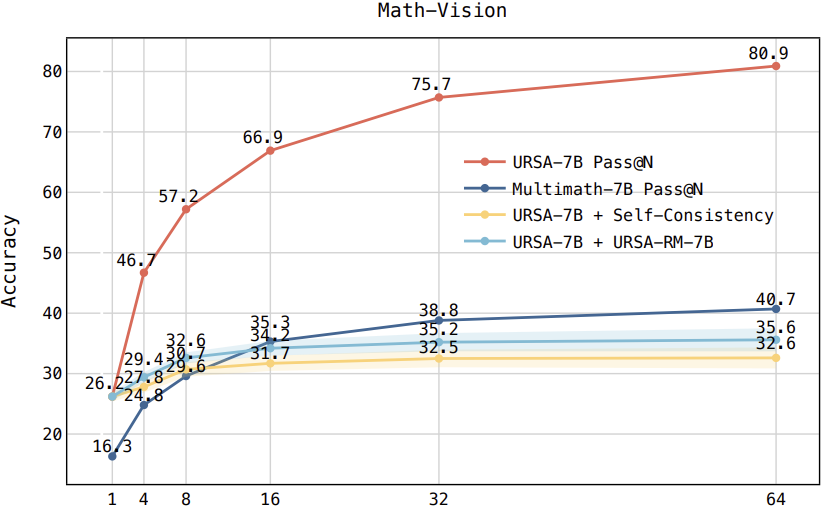
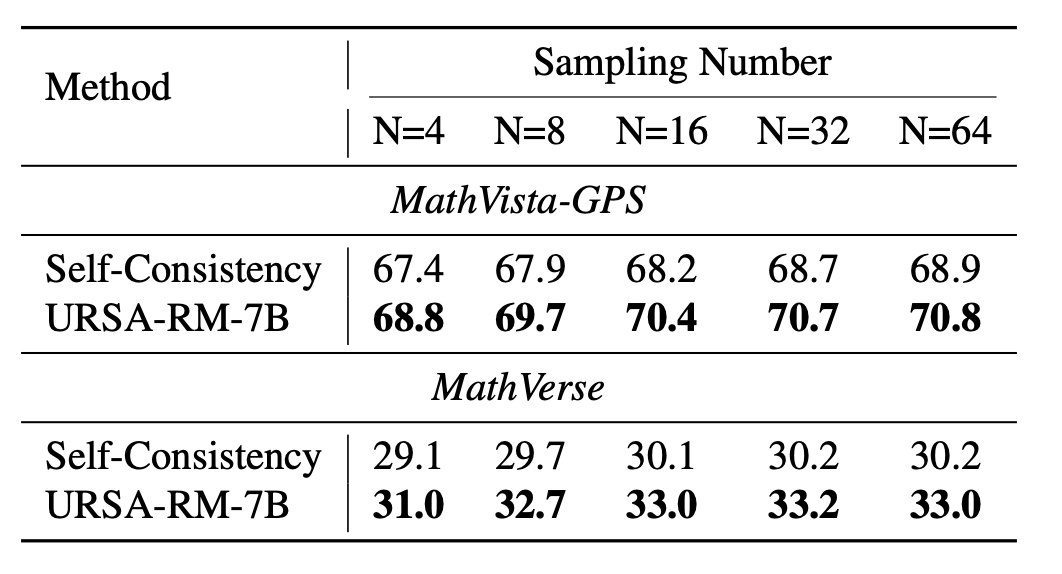
Accuracy scores on the testmini subset of MathVista (1,000 examples) and MathVerse (4,728 examples).
| Model | MathVista | MathVerse | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ALL | GPS | MWP | FQA | TQA | VQA | ALL | TD | TL | TO | VI | VD | VO | |
| Baselines | |||||||||||||
| Random | 17.9 | 21.6 | 3.8 | 18.2 | 19.6 | 26.3 | 12.4 | 12.4 | 12.4 | 12.4 | 12.4 | 12.4 | 12.4 |
| Human | 60.3 | 48.4 | 73.0 | 59.7 | 63.2 | 55.9 | 64.9 | 71.2 | 70.9 | 41.7 | 61.4 | 68.3 | 66.7 |
| Closed-Source MLLMs | |||||||||||||
| GPT-4o | 63.8 | - | - | - | - | - | - | - | - | - | - | - | - |
| GPT-4V | 49.9 | 50.5 | 57.5 | 43.1 | 65.2 | 38.0 | 54.4 | 63.1 | 56.6 | 60.3 | 51.4 | 32.8 | 50.3 |
| Gemini-1.5-002-Flash | 58.4 | - | - | - | - | - | - | - | - | - | - | - | - |
| Gemini-1.5-Pro | 63.9 | - | - | - | - | - | 35.3 | 39.8 | 34.7 | 44.5 | 32.0 | 36.8 | 33.3 |
| Claude-3.5-Sonnet | 67.7 | - | - | - | - | - | - | - | - | - | - | - | - |
| Qwen-VL-Plus | 43.3 | 35.5 | 31.2 | 54.6 | 48.1 | 51.4 | 21.3 | 26.0 | 21.2 | 25.2 | 18.5 | 19.1 | 21.8 |
| Open-Source General MLLMs | |||||||||||||
| mPLUG-Owl2-7B | 22.2 | 23.6 | 10.2 | 22.7 | 27.2 | 27.9 | 10.3 | 11.6 | 11.4 | 13.8 | 11.1 | 9.4 | 8.0 |
| MiniGPT4-7B | 23.1 | 26.0 | 13.4 | 18.6 | 30.4 | 30.2 | 12.2 | 12.3 | 12.9 | 13.4 | 12.5 | 14.8 | 8.7 |
| LLaVA-1.5-13B | 27.7 | 22.7 | 18.9 | 23.8 | 43.0 | 30.2 | 12.7 | 17.1 | 12.0 | 22.6 | 12.6 | 12.7 | 9.0 |
| SPHINX-V2-13B | 36.7 | 16.4 | 23.1 | 54.6 | 41.8 | 43.0 | 16.1 | 20.8 | 14.1 | 14.0 | 16.4 | 15.6 | 16.2 |
| LLaVA-NeXT-34B | 46.5 | - | - | - | - | - | 34.6 | 49.0 | 37.6 | 30.1 | 35.2 | 28.9 | 22.4 |
| InternLM-XComposer2-VL-7B | 57.6 | 63.0 | 73.7 | 55.0 | 56.3 | 39.7 | 25.9 | 36.9 | 28.3 | 42.5 | 20.1 | 24.4 | 19.8 |
| Deepseek-VL | 34.9 | 28.4 | 55.9 | 26.8 | 32.9 | 34.6 | 19.3 | 23.0 | 23.2 | 23.1 | 20.2 | 18.4 | 11.8 |
| LLaVA-OneVision-7B | 58.6 | 71.6 | 69.4 | 51.3 | 56.3 | 45.3 | - | - | - | - | - | - | 26.9 |
| Qwen2-VL | 58.9 | 40.9 | 64.0 | 69.1 | 60.1 | 58.1 | 33.6 | 37.4 | 33.5 | 35.0 | 31.3 | 30.3 | 28.1 |
| InternVL2-8B | 58.3 | 62.0 | 59.1 | 58.7 | 61.4 | 49.7 | 35.9 | 39.0 | 33.8 | 36.0 | 32.2 | 30.9 | 27.7 |
| InternVL2.5-8B | 64.5 | 64.9 | 70.4 | 63.2 | 66.5 | 58.1 | - | - | - | - | - | - | 22.8 |
| Open-Source Math MLLMs | |||||||||||||
| G-LLaVA-7B | 25.1 | 48.7 | 3.6 | 19.1 | 25.0 | 28.7 | 16.6 | 20.9 | 20.7 | 21.1 | 17.2 | 14.6 | 9.4 |
| Math-LLaVA-13B | 46.6 | 57.7 | 56.5 | 37.2 | 51.3 | 33.5 | 22.9 | 27.3 | 24.9 | 27.0 | 24.5 | 21.7 | 16.1 |
| Math-PUMA-Qwen2-7B | 47.9 | 48.1 | 68.3 | 46.5 | 46.2 | 30.2 | 33.6 | 42.1 | 35.0 | 39.8 | 33.4 | 31.6 | 26.0 |
| Math-PUMA-DeepSeek-Math | 44.7 | 39.9 | 67.7 | 42.8 | 42.4 | 31.3 | 31.8 | 43.4 | 35.4 | 47.5 | 33.6 | 31.6 | 14.7 |
| MAVIS-7B | - | 64.1 | - | - | - | - | 35.2 | 43.2 | 37.2 | - | 34.1 | 29.7 | 31.8 |
| InfiMM-Math | - | - | - | - | - | - | 34.5 | 46.7 | 32.4 | - | 38.1 | 32.4 | 15.8 |
| MultiMath-7B | 50.0 | 66.8 | 61.8 | 40.1 | 50.0 | 33.0 | 27.7 | 34.8 | 30.8 | 35.3 | 28.1 | 25.9 | 15.0 |
| Ours | |||||||||||||
| URSA-8B | 59.8 | 79.3 | 75.3 | 44.6 | 63.9 | 40.2 | 45.7 | 55.3 | 48.3 | 51.8 | 46.4 | 43.9 | 28.6 |
| ∆ over SOTA Open-Source Math MLLMs | +9.8 | +12.5 | +7.0 | -1.9 | +12.6 | +6.7 | +10.5 | +8.6 | +11.1 | +4.3 | +8.3 | +11.5 | -3.2 |
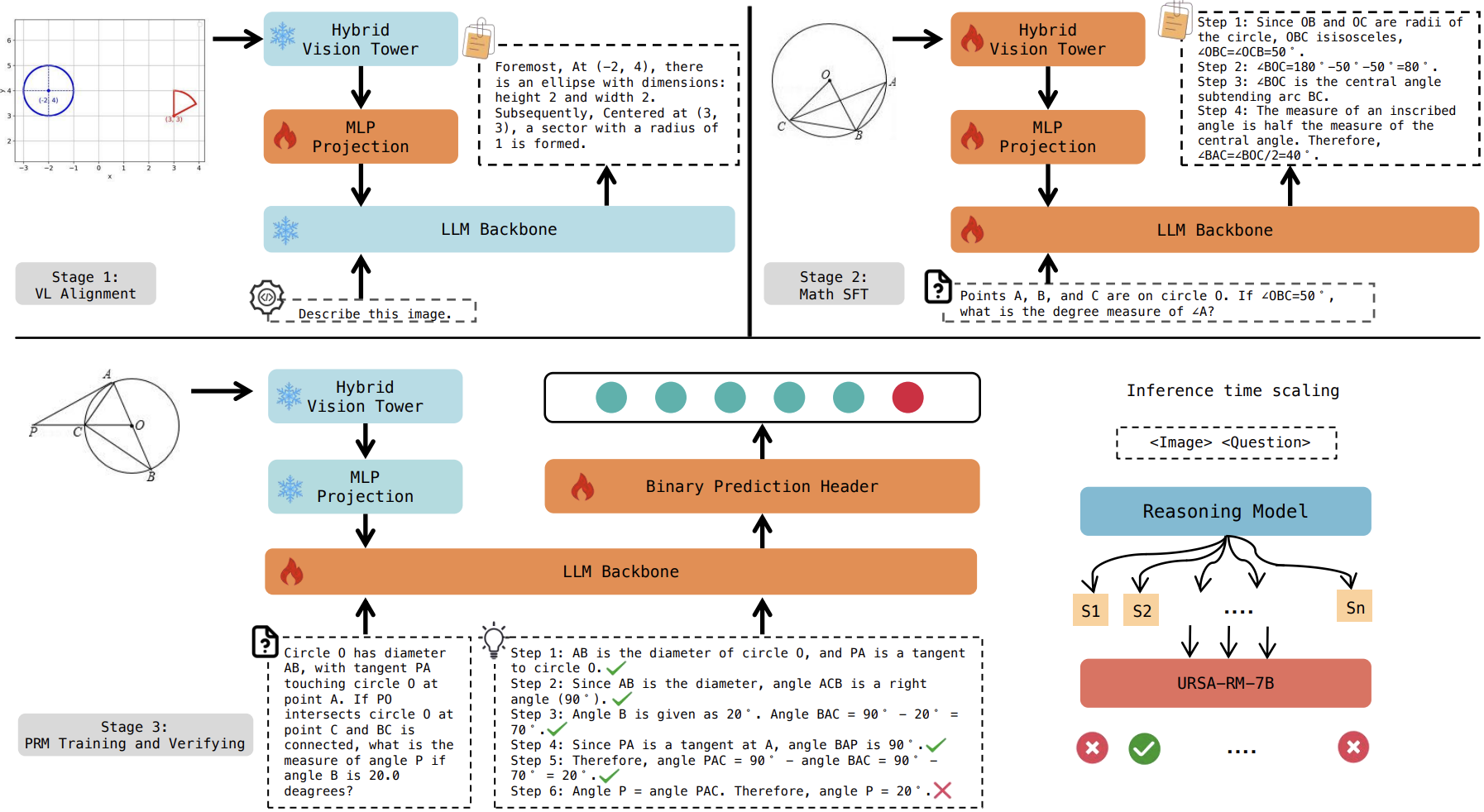
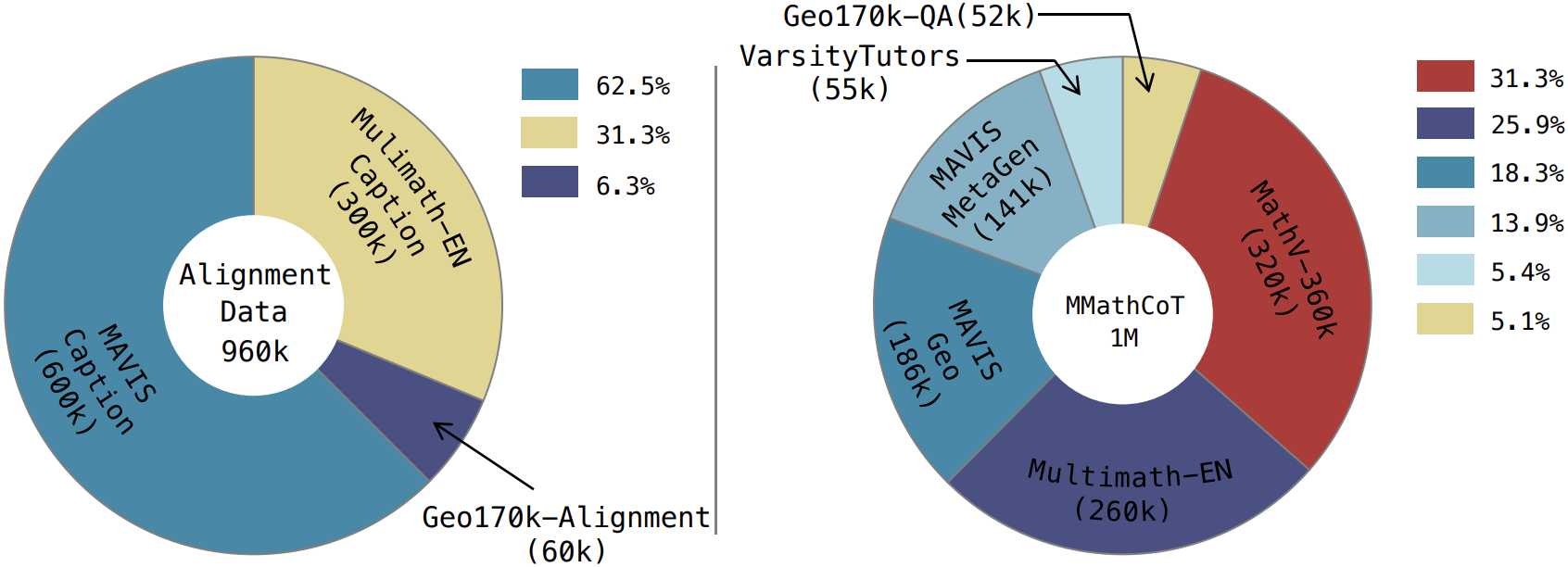
 URSA:
URSA: